圆的标准方程
圆的定义： 圆是平面内到定点的距离为定长的点的轨迹，定点叫做圆心，定长叫做半径。 圆的标准方程： 设圆心的坐标为（a,b），半径为r，(x,y)为圆上的任意一点，则圆的标准方程为：（x-a）²+(y-b)²=r²
特别的，当圆心为坐标原点O（0,0)时，半径为r的圆的标准方程为：x²+y²=r²
圆的一般方程
圆的一般方程：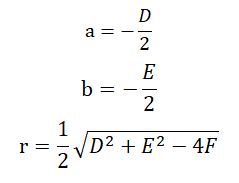
这是一个二元二次方程，它具有下列特点：
（1）含x²项的系数与含y²项的系数都是1；
（2）方程不含xy项。
*方程中的D、E、F均为常数。
一般方程与标准方程的关系：
（1）
（2）标准方程易于看出圆心与半径
直线与圆的位置关系
平面内直线与圆的位置关系有三种： （1）相离：无交点； （2）相切：仅有一个交点； （3）相交：有两个交点。 直线与圆的位置关系和圆心到直线的距离d与半径r的关系： （1）d>r：直线与圆相离； （2）d=r：直线与圆相切； （3）d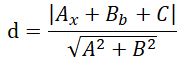
的距离为：
比较d与r的大小，就可以判断直线与圆的位置关系。